Il sistema e l’automa (ASF)
Stati, ingressi/uscite, transizioni, tabelle e diagrammi
Che cos’è un sistema (e che cos’è un automa)
Un sistema è un insieme organizzato di parti che, ricevendo degli ingressi, produce delle uscite tramite un processo di elaborazione. Un automa è un modello (spesso matematico) che descrive un sistema con memoria limitata, in cui il comportamento dipende dallo stato in cui si trova.
Nella rappresentazione a scatola nera non interessa “come è fatto dentro” il sistema, ma solo cosa riceve in ingresso e cosa produce in uscita, e quali stati può assumere.
Un’automobile può essere vista come un sistema che cambia “stato” (ferma, in marcia, ecc.) in base a ingressi (acceleratore, marcia, freno…) e produce uscite (movimento, consumi, emissioni…).

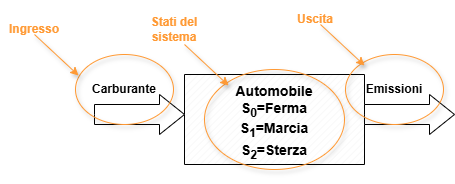
Lo stato del sistema
Lo stato del sistema descrive le condizioni interne in cui si trova il sistema in un determinato istante. In pratica è “la memoria” che serve per capire cosa farà il sistema quando riceve un ingresso.
Cosa succede “dentro” il sistema? Come si passa da uno stato ad un altro quando arriva un ingresso? Per descriverlo in modo rigoroso si usano funzioni e rappresentazioni (tabella e diagramma).
Modello matematico: transizione e uscita
Un sistema a stati (e quindi un automa) si descrive con due leggi fondamentali: una per il cambio di stato e una per la produzione delle uscite.
Indica come cambia lo stato in base allo stato attuale e all’ingresso ricevuto.
s(t) = f(s(t-1), i(t))
Indica quale uscita produce il sistema in base allo stato e (in generale) all’ingresso.
u(t) = g(s(t), i(t))
Un sistema a stati può essere descritto formalmente con questi insiemi:
Ingressi: I = { i0, i1, i2, ... }
Uscite: U = { u0, u1, u2, ... }
Stati: S = { s0, s1, s2, ... }
Transizione: f( )
Uscita: g( )
Sistema = (I, U, S, f(), g())
Classificazione dei sistemi (ripulita e chiara)
- Variante: a parità di ingresso, il comportamento può cambiare nel tempo (il sistema evolve).
- Invariante: a parità di ingresso e condizioni, il comportamento resta lo stesso.
- Continuo: le grandezze possono assumere infiniti valori (es. reali).
- Discreto: le grandezze assumono valori “contabili” o finiti (es. naturali, livelli logici).
- Dinamico: lo stato cambia al variare degli ingressi (tipico degli automi).
- Statico: lo stato non cambia (o non è rilevante) anche se arrivano stimoli.
- Deterministico: dato stato+ingresso, il risultato è prevedibile e unico.
- Stocastico: l’evoluzione dipende anche da fattori probabilistici.
- Combinatorio: le uscite dipendono solo dagli ingressi del momento (nessuna memoria).
- Sequenziale: le uscite dipendono dagli ingressi e anche dallo stato (quindi dalla “storia”).
L’automa e l’Automa a Stati Finiti (ASF)
Un automa è un modello che simula matematicamente il funzionamento di un dispositivo reale progettato per raggiungere un obiettivo (risolvere un problema). Prima di costruire il dispositivo vero, spesso si costruisce il modello (l’automa) per capirne e verificarne il comportamento.
Di solito si definiscono: S0 (stato iniziale) e, quando serve, uno o più stati finali (stati di “accettazione” o fine processo).
In un sistema digitale lo stato può essere memorizzato tramite variabili di stato (bit). Se ho n bit, posso rappresentare fino a 2n stati.
Condizione di codifica: 2^n ≥ numero_stati
Esempio completo: distributore automatico di bibite
Consideriamo un distributore che eroga una bibita dal valore di 1€ e accetta solo monete da 0,50€. L’ingresso è quindi sempre “inserita moneta da 0,50€”.
Ingressi:
I = { I1 = moneta_0_50 }
Uscite:
U = { U1 = eroga_bibita }
Stati:
S = { S1, S2 }
S1: attesa 1ª moneta (stato iniziale)
S2: attesa 2ª moneta
- In S1, arriva I1 → vado in S2, non esce nulla.
- In S2, arriva I1 → torno in S1, ed esce la bibita.
Le righe sono gli stati, le colonne gli ingressi. In ogni cella mettiamo: (stato successivo, uscita).
| Stato attuale | I1 = moneta 0,50€ |
|---|---|
| S1 (attesa 1ª moneta) | S2, nessuna uscita |
| S2 (attesa 2ª moneta) | S1, eroga bibita |
Diagramma degli stati: come si rappresenta un automa
Un automa può essere rappresentato con un diagramma degli stati (un grafo): i nodi sono gli stati, gli archi sono le transizioni. Su ogni freccia si indica la coppia ingresso/uscita.


Mealy e Moore (differenza essenziale)
Esistono due modelli principali di automi: Moore e Mealy. La differenza sta in da cosa dipende l’uscita.
L’uscita dipende solo dallo stato.
Moore: u(t) = g(s(t))
L’uscita dipende da stato e ingresso.
Mealy: u(t) = g(s(t), i(t))
Riepilogo
Funzioni di Transizione e di Trasformazione
La funzione di transizione descrive come cambia lo stato del sistema in base agli ingressi, mentre la funzione di trasformazione determina le uscite del sistema in base allo stato attuale e agli ingressi ricevuti.
Funzione di transizione: s(t) = f(s(t₀), i(t))
Funzione di trasformazione: u(t) = g(s(t), i(t))



Automa a Stati Finiti
Un Automa a Stati Finiti (ASF) è un automa con un numero finito di stati. Ogni stato è associato a determinati ingressi e uscite, e la transizione tra gli stati dipende dagli ingressi ricevuti.
Esempio: Distributore Automatico di Bibite
Un esempio classico di ASF è un distributore automatico che eroga bibite. Questo sistema può essere rappresentato come un automa a stati finiti, con stati come "Attesa della moneta" e "Attesa della seconda moneta".
Tabella di Transizione
La tabella di transizione descrive come l'automa cambia stato in funzione degli ingressi ricevuti.
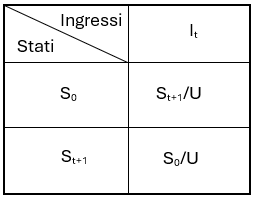
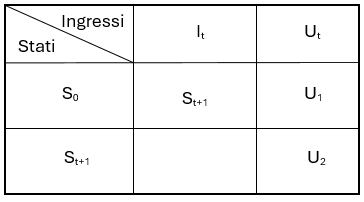
Riepilogo
- Un automa è un sistema che cambia stato in base agli ingressi ricevuti.
- Un Automa a Stati Finiti (ASF) ha un numero limitato di stati, determinati dalla sua tabella di transizione.
- Le uscite del sistema dipendono sia dallo stato che dagli ingressi.